エルミート曲線 (Hermite Curve)
最近はあまり使われないようですが、処理が軽くシンプルな3次エルミート曲線。各点にベクトルを持ち、2つの点と2つのベクトルから2点を結ぶカーブが取得できる。パラメータt\((0 \leq t \leq 1)\)を変えることにより2点の間の位置が取得可能。
式は通常3次多項式から作られ、その式の微分(tにおけるその位置での加速度)とで解いていくと式が得られる。
ほとんど参考サイトとをなぞっているだけですが、数式の出し方は以下。
まずは3次多項式とその微分を用意。
\begin{align}
P(t) &= at^3 + bt^2 + ct + d\\
P'(t) &= 3at^2 + 2bt + c\\
& (0 \leq t \leq 1)
\end{align}
上記の式に t=0 と t=1 の値を代入。
また微分したものを\(v_0\)、\(v_1\)とする。
\begin{align}
& P(0) = d & P'(0) = c = v_0\\
& P(1) = a + b + c + d & P'(1) = 3a + 2b + c = v_1\\
\end{align}
上記の式を展開。
\begin{align}
\left\{
\begin{array}{ll}
& a + b = P(1) – v_0 – P(0)\\
& 3a + 2b = v_1 – v_0
\end{array}
\right.
\end{align}
上記の式を展開。
\begin{align}
b &= P(1) – v_0 – P(0) – a\\
\\
3a + 2b &= 3a + 2(P(1) – v_0 – P(0) – a)\\
&= a + 2P(1) – 2v_0 – 2P(0)\\
&= v_1 – v_0\\
\\
a &= v_1 – v_0 -2P(1) + 2v_0 + 2P(0)\\
&= v_1 + v_0 – 2P(1) + 2P(0)
\\
b &= P(1) – v_0 – P(0) – a\\
&= P(1) – v_0 – P(0) – (v_1 + v_0 – 2P(1) + 2P(0))\\
&= 3P(1) – 2v_0 – 3P(0) – v_1\\
\end{align}
a, bは上記から。c, dは最初の方に導き出されているので、a, b, c, dが揃った。それぞれを最初の3次多項式に入れて完成。
\begin{align}
f(t) = (2P(0) – 2P(1) + v_0 + v_1)t^3 + (-3P(0) + 3P(1) – 2v_0 – v_1)t^2 + v_0t + P(0)
\end{align}
参考)
Qiita | ゲームプログラマのためのパラメトリック曲線入門(Hermite Curve)
t-pot | 3次曲線
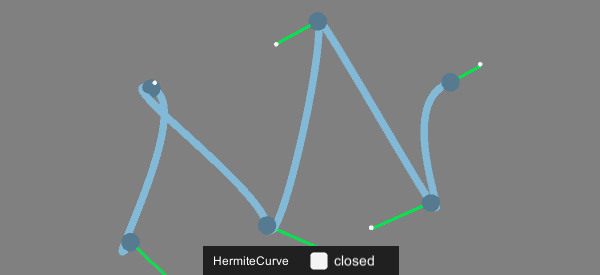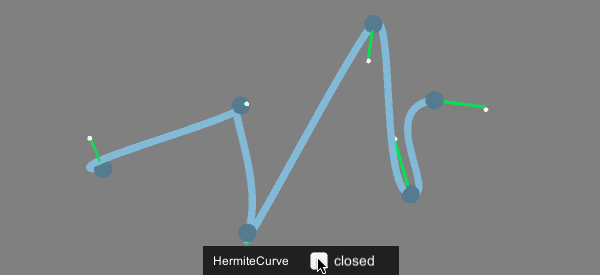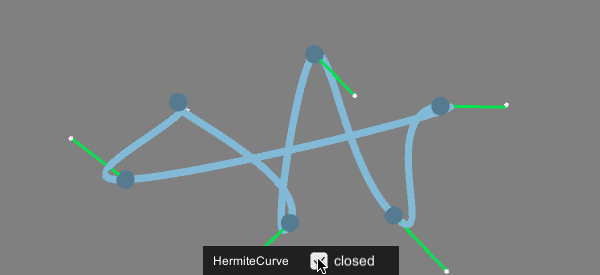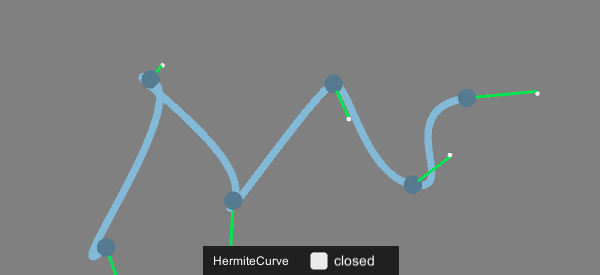
[…] エルミート曲線 (Hermite Curve) 各点において次の線がどのベクトルへ向かうかを持った曲線。 […]
[…] Catmull-Romスプライン曲線は制御点を必要とせず、全ての点を通る曲線。エルミート曲線での各点のベクトルに対して下記のように前後の点の位置からベクトルを自動的に作ったもの入れ […]