B-スプライン曲線 (B-spline Curve)
B-スプライン曲線はベジェ曲線と違い、点を通らない。その代わり曲線同士の曲率(曲がり具合)が連続していて滑らかな曲線となる。曲線は基底関数を重ね合わせて表現され、重ね合わせる具合をノットという数値の集合で表す。ノットの数は制御点の数+次数+1となる。(次数+1を階数(order)と呼ぶ)
ノットの値は絶対的な数値ではなく、複数の基底関数を重ね合せる祭の相対的な数値の列であり、B-スプライン曲線では通常ノット値を0からはじめ、1ずつ増やして等間隔にする。(uniform:一様)
制御点6で次数が3の場合は10個のノット値があり
\([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]\)
となる。
ノット値の条件は \(knot[n-1] \leq knot[n] < knot[n+1]\) となり同じ数値を次数+1回だけ重ねることができる。次数+1だけ重ねるとその点を通ることとなり始点と終点を通る場合を開一様(open-uniform)と呼ぶ。先の条件では
\([0, 0, 0, 0, 1, 2, 3, 3, 3, 3]\)
となる。
こちらが一様のグラフ。
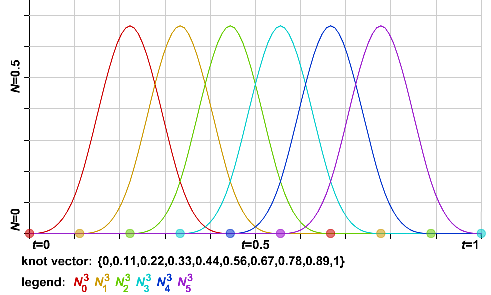
こちらが開一様のグラフ。始点と終点を通るので最初の方のノットと最後の方のノットが重なっている状態。
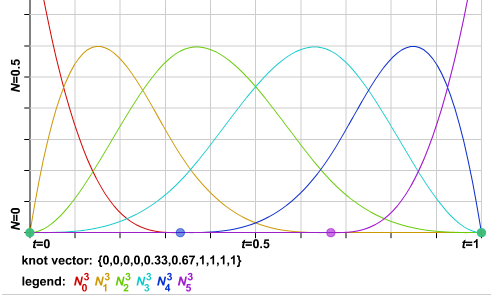
引用) http://geometrie.foretnik.net/files/NURBS-en.swf
(上図ではノットが1ずつの増加ではなく、0〜1の間で等間隔に配置しているが、意味は同じ)
曲線の定義は制御点の数を\(m\)、次数を\(n\)、B-スプライン基底関数を\(b_i^n(t)\)とすると
\begin{align}
P(t) = \sum_{i=0}^{m-1}b_i^n(t)P_i
\end{align}
Bスプライン基底関数は
\begin{align}
b_j^0(t) =&
\left\{
\begin{array}{ll}
& 1 & (t_j \leq t < t_{j+1})\\
& 0 & otherwise
\end{array}
\right.\\
b_j^n(t) =& \frac{t - t_j}{t_{j+n} - t_j}b_j^{n-1}(t) + \frac{t_{j+n+1}-t}{t_{j+n+1}-t_{j+1}}b_{j+1}^{n-1}(t)
\end{align}
(分母が0となる場合にはその項を0とする)
また、ノットの範囲は
\begin{align}
t_n \leq t \leq t_{m}
\end{align}
となる。
これをこちらの資料にあるこちらのプログラムを参考に実装すればOK。
ベジェ曲線同様、よく使う2次と3次をあらかじめ計算しておくと早そうなので。
2次の場合はまずノット列が
\begin{align}
[0, 1, 2, 3, 4, 5]
\end{align}
これを式がシンプルになるように次数分だけマイナスさせておくと
\begin{align}
[-2, -1, 0, 1, 2, 3]
\end{align}
そして曲線の式が
\begin{align}
P(t) &= \sum_{i=0}^2b_i^2(t)P_i\\
&= b_0^2(t)P_0 + b_1^2(t)P_1 + b_2^2(t)P_2
\end{align}
となるので、\(b_0^2, b_1^2, b_2^2\)が分かればOK。
またノットの範囲は(\(t_2 \leq t \leq t_3 = 0 \leq t \leq 1\))となるので、計算するのは下記の赤い範囲で、それ以外は0。
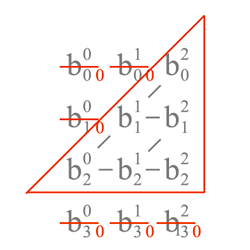
まずは\(b_2^0\)は1になるので、次に\(b_2^1\)を求めると
\begin{align}
b_2^1 &= \frac{t-t_2}{t_3-t_2}b_2^0(t) + \frac{t_4-t}{t_4-t_3}b_3^0(t)\\
&= (t-t_2)1 + (t_4-t)0\\
& = t
\end{align}
続いて\(b_1^1\)を求めると
\begin{align}
b_1^1 &= \frac{t-t_1}{t_2-t_1}b_1^0(t) + \frac{t_3-t}{t_3-t_2}b_2^0(t)\\
&= (t-t_1)0 + (t_3-t)1\\
&= 1 – t
\end{align}
引き続き\(b_2^2\)
\begin{align}
b_2^2 &= \frac{t-t_2}{t_4-t_2}b_2^1(t) + \frac{t_5-t}{t_5-t_3}b_3^1(t)\\
&= \frac{t-t_2}{2}(t) + \frac{t_5-t}{2}0\\
&= \frac{t^2}{2}
\end{align}
\(b_1^2\)は
\begin{align}
b_1^2 &= \frac{t-t_1}{t_3-t_1}b_1^1(t) + \frac{t_4-t}{t_4-t_2}b_2^1(t)\\
&= \frac{t-t_1}{2}(1 – t) + \frac{t_4-t}{2}(t)\\
&= \frac{(t+1)(-t+1)}{2} + \frac{(2-t)t}{2}\\
&= \frac{-t^2+1}{2} + \frac{-t^2+2t}{2}\\
&= \frac{-2t^2+2t+1}{2}
\end{align}
最後に\(b_0^2\)
\begin{align}
b_0^2 &= \frac{t-t_0}{t_2-t_0}b_0^1(t) + \frac{t_3-t}{t_3-t_1}b_1^1(t)\\
&= \frac{t-t_0}{2}0 + \frac{t_3-t}{2}(1-t)\\
&= \frac{(1-t)(1-t)}{2}\\
&= \frac{t^2-2t+1}{2}
\end{align}
これで2次の曲線の式が下記のようになる。
\begin{align}
P(t) &= b_0^2(t)P_0 + b_1^2(t)P_1 + b_2^2(t)P_2\\
&= \frac{1}2(t^2-2t+1)P(0) + \frac{1}{2}(-2t^2+2t+1)P(1)+\frac{1}{2}t^2P(2)
\end{align}
同じように3次を展開すると、こちらのようになる
3次
\begin{align}
P(t) = \frac{1}{6}(1-t)^3P(0) + (\frac{1}{2}t^3+t^2+\frac{2}{3})P(1) + (-\frac{1}{2}t^3+\frac{1}{2}t^2+\frac{1}{2}t+\frac{1}{6})P(2) + \frac{1}{6}t^3P(3)
\end{align}
参考)
B-スプライン曲線の一考察
SFC Design theory 2012 6/20
Open Processing | N-BSpline
t-pot | 3次曲線 | B-Spline曲線
AFSoft | CADを考える:スプライン(5)
3次元図形処理技術解説 第10回 B-Spline曲線(3)
Architektura, geometrie a výpočetní technika | NURBSdemo (swf)
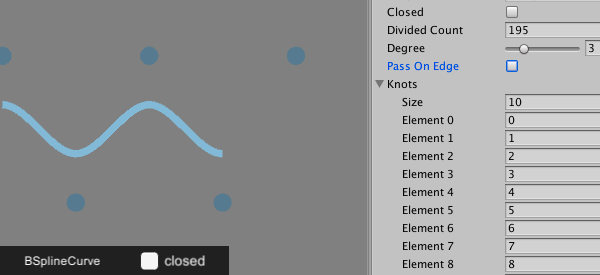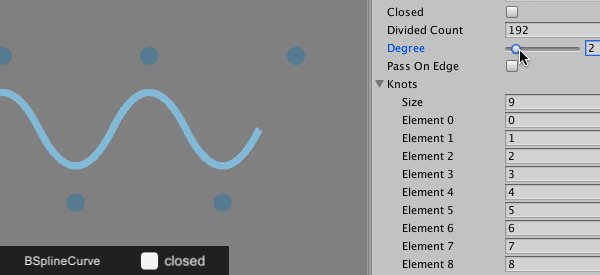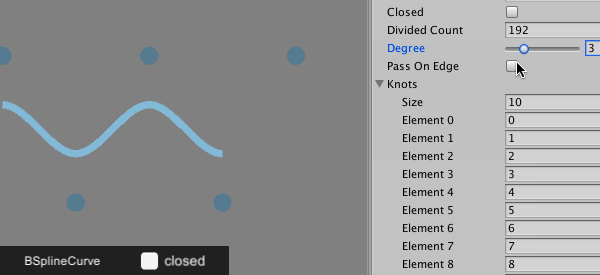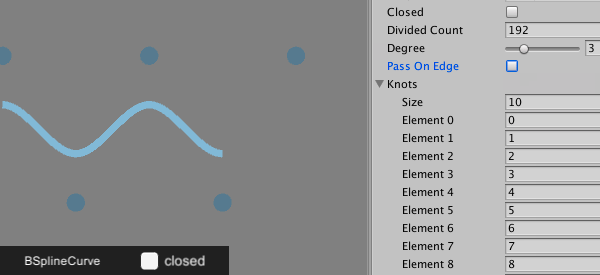
[…] バースタイン基底関数は前回の投稿同様で、曲線の定義は制御点の数を\(m\)、階数を\(n\)、B-スプライン基底関数を\(b_i^n(t)\)とすると […]