Tweet

github | naochang | Curve
Illustrator等でもおなじみのベジェ曲線。ベジェ曲線には次数があり、Illustratorでは3次、Flashでは絵を描くときは3次だけど、実行するときは2次に変換される。(FlashPlayer11以降は3次もサポート)
次数が大きいほど制御点が多く、少ないアンカーポイントで線を調整ができるが、処理も重たくなる。

どのような仕組みかは、こちらのアニメーションgifを見るとわかりやすい。

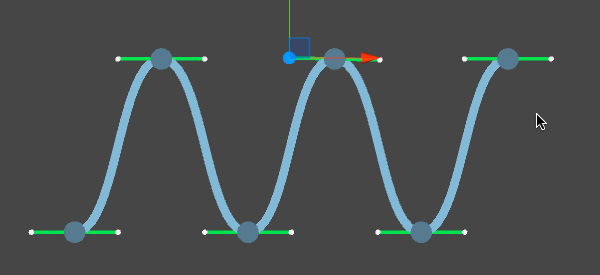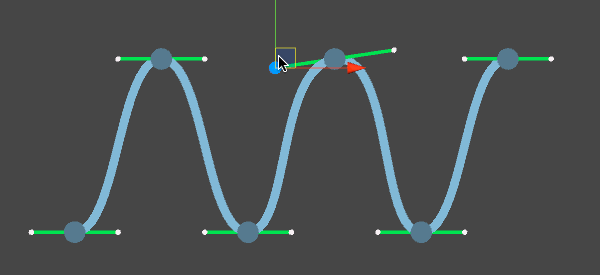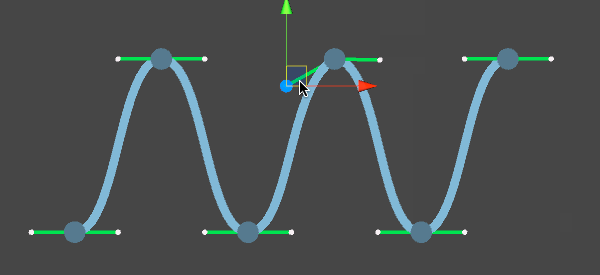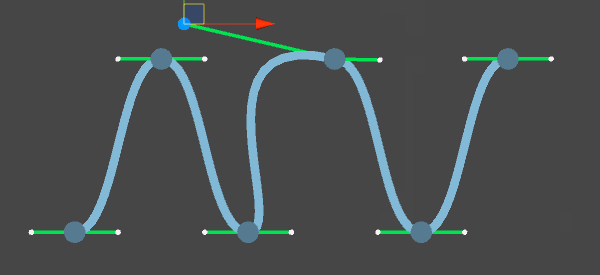
3次の場合は点が4つ必要になり、通るのは始点と終点のみ。残りの2点は曲線を制御するために使われる。Illustratorなどでいうところのハンドルがそれにあたる。3次の場合は4つの始点と終点のみ繋いでいくので、それを最初の点から最後の点まで繰り返して、複数の点がなめらかに繋がるように見せるが、線が滑らかになるように点にある2つのハンドルが点を挟んで線対称となるように配置する。線対称でない場合は、Illustratorでいうハンドルを折っている状態で、滑らかではなくなる。逆にこう行った操作が容易にできるベジェ曲線は特に2Dを描くのに向いているんですね。

曲線ではどのように滑らかな曲線を作るかというブレンディング関数があり、ベジェ曲線ではバーンスタイン基底関数というブレンディング関数を使っているようです。ベジェ曲線の式を見て見ると。

\begin{align}
P(t) = \sum_{i=0}^{N-1}P_iB_{(N-1)i}(t)
\end{align}

\(P_i\)は制御点、\(N\)は制御点の数。\(B_ni(t)\)がバーンスタイン基底関数。バーンスタイン基底関数は
\begin{align}
B_{ni}(t) = { n \choose i }t^i(1 – t)^{n-i}
\end{align}

ここで\({n \choose i}\)は二項係数で、組み合わせと同じ。
\begin{align}
{n \choose k} = \frac{n!}{k!(n-k)!}
\end{align}

上記の式をまとめると
\begin{align}
P(t) = \sum_{i=0}^{N-1}P_i(\frac{(N-1)!}{i!((N-1)-i)!})t^i(1 – t)^{(N-1)-i}
\end{align}
制御点の数 – 1 が次数になるので次数をnとして表現するとこうなる。
\begin{align}
P(t) = \sum_{i=0}^nP_i(\frac{n!}{i!(n-i)!})t^i(1 – t)^{n-i}
\end{align}

あとは、すでにこちらで非常にわかりやすくプログラム化されているので、それをなぞるだけ。よく使いそうな2次と3次をあらかじめ展開しておくと、2次の方は
\begin{align}
P(t) &= P_0(\frac{2!}{0! \times 2!})t^0(1-t)^2\\
&+ P_1(\frac{2!}{1! \times 1!})t^1(1-t)^1\\
&+ P_2(\frac{2!}{1!})t^2(1-t)^0\\
&= P_0(1-t)^2 + 2P_1t(1-t) + 2P_2t^2
\end{align}
3次の方は
\begin{align}
P(t) &= P_0(\frac{3!}{0! \times 3!})t^0(1-t)^3\\
&+ P_1(\frac{3!}{1! \times 2!})t^1(1-t)^2\\
&+ P_2(\frac{3!}{2! \times 1!})t^2(1-t)^1\\
&+ P_3(\frac{3!}{3! \times 0!})t^3(1-t)^0\\
&= P_0(1-t)^3 + 3P_1t(1-t)^2 + 3P_2t^2(1-t) + P_3t^3
\end{align}

ハンドルの位置がアンカーポイントの点対象にあれば滑らかなカーブとなるが、位置が違うと折れ曲がったカーブとなる。

参考）
[数学] 3D空間にベジェ曲線を描く
中学生でもわかるベジェ曲線